Calculadora de Integrales

Ingresa arriba la función a integrar. La variable y los límites de integración y demás pueden ser cambiados en "Opciones". Da clic en "Ir" para empezar el cálculo de la integral/antiderivada. El resultado se mostrará más abajo.

Cómo funciona la Calculadora de Integrales

Para aquellos con antecedentes técnicos, la siguiente sección explica cómo funciona la Calculadora de Integrales.

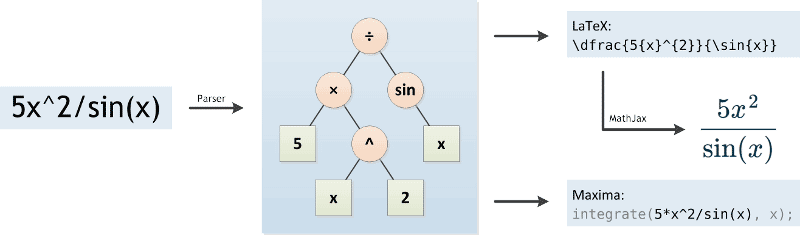
Primero, un analizador sintáctico (o parser) analiza la función matemática. Este la convierte a un formato más comprensible para una computadora, esto es un árbol (veáse figura abajo). Al hacer esto, la Calculadora de Integrales tiene que respetar el orden de operaciones. Algo especial en expresiones matemáticas es que el signo de multiplicación puede ser omitido en ocasiones, por ejemplo escribimos 5x en lugar de 5*x. La Calculadora de Integrales tiene que detectar esos casos e insertar el signo de multiplicación.

El parser está implementado en JavaScript, basado en el algoritmo Shunting-yard, y puede ser ejecutado directamente en el explorador. Esto permite un rápido feedback mientras escribimos al transformar el árbol en código LaTeX. MathJax se encarga de mostrar la función en el explorador.

Cuando el botón "Ir" es presionado, la Calculadora de Integrales envía la función matemática y las opciones de configuración (variable y límites de integración) al servidor, donde es analizada otra vez. Esta vez, la función es transformada a un formato que puede ser entendido por el sistema de álgebra computacional Maxima.

Maxima se encarga en realidad del cómputo de la integral de la función matemática. El resultado de Maxima es transformado a LaTeX otra vez y es presentado entonces al usuario. En muchos casos, la antiderivada es calculada usando el Algoritmo de Risch, el cual es difícil de entender para los humanos. Es por ello que mostrar los pasos del cálculo es muy retador para el caso de integrales.

Para poder mostrar los pasos, la calculadora aplica las mismas técnicas de integración que un humano aplicaría. El programa que realiza esto ha sido desarrollado a lo largo de varios años y está escrito en el propio lenguaje de programación de Maxima. Consiste en más de 17 000 líneas de código. Cuando el integrando coincide con una forma conocida, se aplican reglas establecidas para resolver la integral (p. ej. descomposición en fracciones parciales para funciones racionales, sustitución trigonométrica para integrandos que involucran las raíces cuadradas de un polinomio cuadrado o integración por partes para productos de ciertas funciones). Por lo demás, se intenta con diferentes sustituciones y transformaciones hasta que la integral está resuelta, se termina el tiempo alojado o no queda nada más que intentar. La calculadora carece de la intuición matemática que es tan útil para encontrar una antiderivada, pero por otro lado puede probar un gran número de posibilidades en un tiempo muy corto. Las antiderivadas paso a paso son frecuentemente mucho más cortas y más elegantes que aquellas encontradas por Maxima.

La función "Verifica la respuesta" tiene que resolver la difícil tarea de determinar si dos expresiones matemáticas son equivalentes. Su diferencia se calcula y simplifica tanto como sea posible usando Maxima. Por ejemplo, esto implica escribir funciones trigonométricas/hiperbólicas en sus formas exponenciales. Si se puede demostrar que la diferencia es cero, la tarea está resuelta. De otra manera, se aplica un algoritmo probabilístico que evalúa y compara ambas funciones en lugares determinados aleatoriamente. El el caso de antiderivadas, el procedimiento entero se repite con la derivada de cada función, ya que las antiderivadas pueden diferir por una constante.

Las gráficas interactivas de funciones son calculadas en el explorador y se muestran dentro de un lienzo, también llamado elemento canvas (HTML5). Por cada función a graficar, la calculadora crea una función de JavaScript, que es finalmente evaluada en intérvalos pequeños a fin de dibujar la gráfica. Al dibujar las gráficas, las singularidades matemáticas (p. ej. polos) son detectadas y tratadas especialmente. El control de gestos se implementó usando Hammer.js.

Si tienes cualquier pregunta o ideas para mejorar la Calculadora de Integrales, no dudes en escribirme un e-mail.